抵抗器の部分は,電球でもモータでもLEDでも,何でもいいってことだ.
まず前提として,以下のことはわかっているとして,話を進めるよ.
・抵抗:電気の流れにくさのこと.記号はR 単位はΩ
あーる おーむ
・オームの法則:電圧Vと電流Iは比例する.V=RI I=
・電熱線やセメント抵抗を使ってオームの法則の実験(「オームの法則の実験」でググろう)をして,
電圧Vと電流Iの関係をグラフにすると,VとIが比例していることがわかる(V=RIの関係になる).
つまり,抵抗Rは一定である.
A君「オームの法則は,V=IRの方がわかりやすいよ.」
B君「数学的に同じなら,別に何でも構わないよ.まあ僕は,VとIが比例する ってわかる形式が好きだね.」
A君「確かに,V=RI,I= の形なら,VとIが比例するってことがわかりやすいよね.」
A君「ところでさ,何で抵抗Rは,電流の流れ「にくさ」の値なの?比例の関係なんだから,電流の流れ「やすさ」で定義してもよかったんじゃん.オームさんって,ひねくれてるの?」
B君「いや,そこがオームさんのすごいところなんだ.
「抵抗は電流の流れにくさ」なのは物理的には正しい定義だが,そのように考えているうちは,電気回路は永遠に理解できない.」
A君「ええ?」
B君「それをこれから,水流モデルを使って説明していこう.」
すべての電気製品は,抵抗器だ.モータも電球もスマホも蛍光灯も,みんな抵抗器だ.
たとえば,電球を2個直列にした回路は,抵抗器の記号を使って,こんな風に書くことができる.
抵抗器の部分は,電球でもモータでもLEDでも,何でもいいってことだ.
A君「てことは,すべての電気製品には抵抗があるってこと?」
B君「その通り.すべての電気製品には抵抗がある.そして,その抵抗の値は,電気製品により決まっている.
たとえば2.5V用の豆電球はだいたい8Ωくらいだし,3.8V用の豆電球は13Ωくらいだ.
学校のソーラーモーターは15Ωくらいかな.まあ個体差はけっこうある.」
電気回路をイメージで理解する秘訣は,実は,暗算だったりする.
A君「なんでよ?」
B君「図に書いてない値を暗算で計算したりすれば,イメージをつかみやすくなるでしょ.」
今回は,暗算の練習をしよう.
(1)V=10V,R=250Ωだ.Iは何mA?
I=V/R=10V÷250Ω=0.04A おっと,mAで答えるのか.答は40mA
(2)R=2kΩ,I=30mAだ.Vはいくつ?
うーん,kΩかよ.2kΩ=2000Ω,そして30mA=0.03A なので,V=RI=2000Ω×0.03A=60V
...でもいいんだけどさ,暗算しにくいよね.ここで,
キロ×ミリ=1 ってのは,わかるかい?
なので,V=RI=2kΩ×30mA=60V ほら,暗算でもできるでしょ.
そういう意味では(1)もさ, =ミリ を使えば,
I=V/R=10V÷0.25kΩ=40mA ほら,暗算でさくっと出せるでしょ.
さてここで,
電力の公式P=VIと,オームの法則V=RIを融合してみよう.
電力Pの公式 P= V I …①
(W) (V)(A)
オームの法則 V= R I …②
(V) (Ω)(A)
この2つの公式を組み合わせると,こんな公式が作れる.
①②からVを消去→ P=I2R …③
①②からIを消去→ P= …④ ※うーん P=V2/R をかっこよく分数形式で書きたかったんだけど...
さて,これを使って,暗算の練習つづき.
(3)V=10V,R=250Ωだ.抵抗器の消費電力は?
Iを計算してからPを出す...でもいいんだけどさ,
④式を使えば,電力Pは一発で計算できる.
P=V2/R=(10V)2÷250Ω=0.4W
(4)R=2kΩ,I=30mAだ.抵抗器の消費電力は?
Vを計算してからPを出す...でもいいんだけどさ,
③式を使おう.P=I2R=(30mA)2×2kΩ=1800mW=1.8W
わかるかな.だって,ミリ×ミリ×キロ=ミリ でしょ.
(5)V=5V,R=2kΩだ.抵抗器の消費電力は?そして,電流Iは?
④式を使おう.P=V2/R=(5V)2÷2kΩ=12.5mW
そして,
I=V/R=5V÷2kΩ=2.5mA
つぎに,例題
100Vの電源をつなぐと40Wで光る電球がある.
この電球に40Vの電源をつなぐと,何Wで光るか.
答は,16W...ではない.
ポイント:どんな回路であっても,抵抗Rがわからないなら,まずRを出す.
なぜかって? 抵抗Rは不変だからだ.ぶれない不変の値がわかれば,計算を正確にできるでしょ.
今回,電球のRがわからないので,まずRを計算で出そう.
P=VIより,40W=100V×I I=0.4A
V=RIより,100V=R×0.4A R=250Ω...ってやってもいいけどさ,
④式で一発で出そうぜ.
P=V2/Rより,40W=(100V)2/R R=250Ω
で,電圧を40Vに変えると(電圧を変えようが電流を変えようが,Rは不変),
P=V2/Rより,P=(40V)2/250Ω=6.4W
A君「4割どころか,むちゃくちゃ暗くなるね.」
B君「④式より,P=V2/Rじゃん.Rは不変なので,PはVの2乗に比例するのだ.」
ここで,2つの重要なポイントを話そう.
ポイント1: オームの法則V=RIのVは,「抵抗器の両端の」電圧である.
電池の電圧と同じとは限らない.
今後,「抵抗器の両端のV」っていちいち書くのは大変なので,このHP上では,これを ※V と表現するよ.
※V と書いてあったら, 抵抗器の両端のV と読むんだよ.
A君「万国共通ルール?」 B君「まさか.このHP上だけだよ.」
オームの法則は, ※V=RI だ.
オームの法則 ※V=RI
電力の公式 P=※VI=I2R=
A君「オームの法則だけでなく,電力の公式も,Vは※Vだったのか!」
B君「水流モデル1 の4章の問題演習では,電球の消費電力の計算は,無意識のうちに※Vで計算してたでしょ.」
次は,抵抗だ.
「抵抗は,電流の流れにくさである.」これは物理的には正しい定義であるが,
そう考えているうちは,電気回路は理解できない.
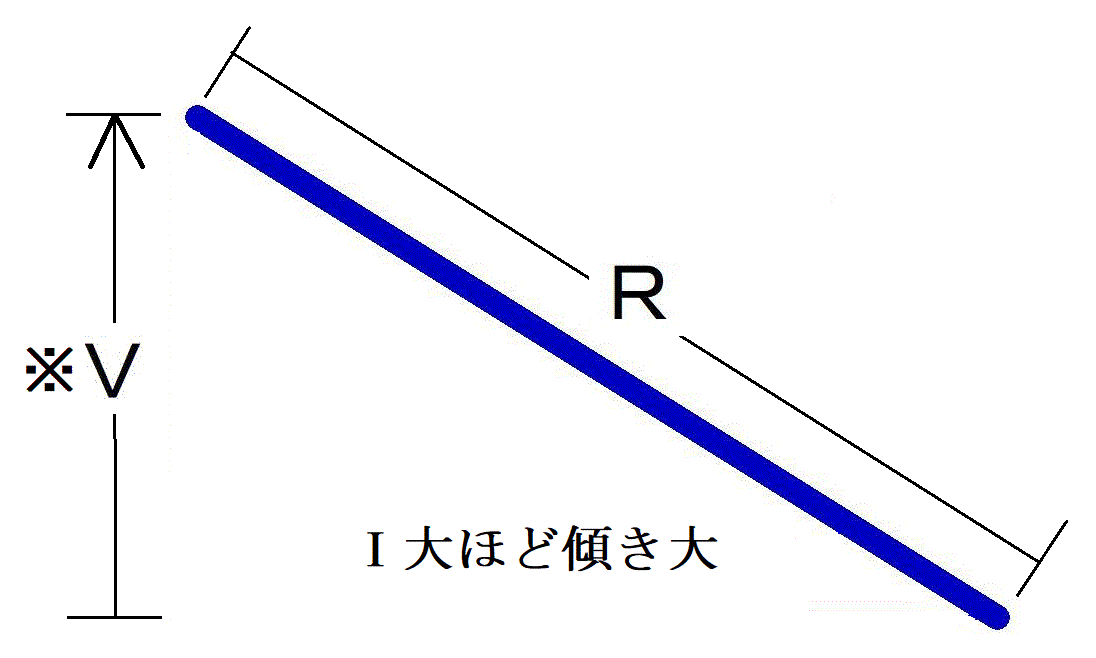 ポイント2: 抵抗とは,(水流モデルの)ななめパイプの長さである.
ポイント2: 抵抗とは,(水流モデルの)ななめパイプの長さである.
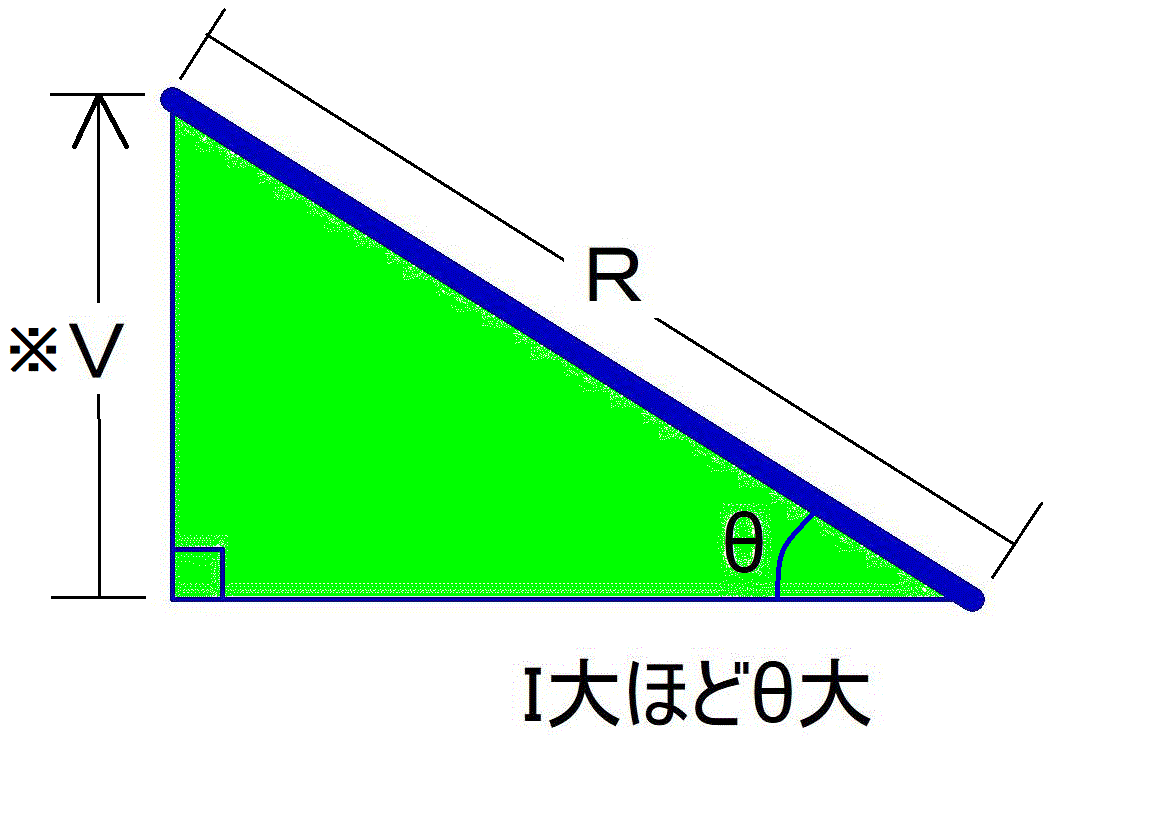
図で表すと,こんな感じである.
ななめパイプを斜辺とする直角三角形の 斜辺がR
垂辺が※V
sinθが,Iだ.
すると, ※V = Rsinθ という関係になるでしょ.
これが,
オームの法則 ※V =RI と対応するのだ.
A君「Iがsinθに相当するの?」
B君「そう.θが0~90°ならsinは単調増加なので,I大ほどθ大 の関係になるでしょ.」
さて, ななめパイプの長さは決まっていて,不変である = Rは不変である.
これはわかるね.
そして,
Rが大(=ななめパイプが長い)だと,少し電流Iが流れるだけで,大きな※Vになる.
そう,電気回路やさんたちは,こういうイメージを持っている.
・抵抗Rとは,※Vをつくりだす電気部品である
・Rが大きいほど,※Vをつくりだす能力が高い.Rが大きければ,少しIが流れるだけで,大きな※Vが得られる.
B君「まあ,うさぎとかめで例えるならば,大きいRは,ウサギだね.能力が高い.
小さいRは,カメさん.」
A君「...わけがわからないよ.」
B君「これがまさに,オームさんの言う専門用語「電圧降下」のイメージなんだ.
回路屋さんたちは,抵抗器を,電流を制限する部品として使うことはほとんどない(たまにはある).
抵抗器は,※Vをつくりだすために使うんだ」
A君「...わけがわからないよ.」
B君「ともかく,抵抗Rは電流の流れにくさ と思っているうちは,電気回路は理解できないよ.」
B君「その一方で,「電池の」電圧Vは決まっているわけだよ.」
A君「つまり,抵抗Rが大きいと,小さい電流Iでも電池の電圧Vとななめパイプの※Vを一致させることができるから,電流Iが小さいってことか.」
B君「そう.能力が高いから,電流Iが小さいのだ. まさに,コースの途中でくつろぐウサギ.」
A君「...わけがわからないよ.」
B君「一方,抵抗Rが小さいと,たくさん電流Iを流さないと電池の電圧Vとななめパイプの※Vを一致させることができないから,電流Iが大きい.
つまり,能力が低いから,電流Iをいっぱい流さないといけないのだ. まさにカメさん.」
A君「...なんでカメはさんづけなの?」
B君「Rが大きいと,電流が流れにくいからIが小さい ってのは物理的な事実だけれど,
電気回路を理解するには,そう考えちゃいけないのよ.」
A君「...わけがわからないよ.」
B君「Rが大きいとIが小さい,というのは,電池と抵抗をつないだ場合だけのことであって,複雑な電気回路のすべての部分がそうなってるわけじゃないでしょ. この考え方からは脱却しないと,電気回路は理解できないよ.」
A君「...わけがわからないよ.」
B君「そんな,さっぱりわけがわからないあなたのために,数学はある.
この正しい抵抗のイメージを,正しく数式で表したもの.それが,オームの法則なんだ.」
オームの法則 ※V=RI には2つの意味がある.
1.※VとIは比例する
2.Rが大きいと,Iが小さくても※Vは十分大きくなる
B君「まさに,今まで語ってきた抵抗のイメージを,数式にしたものなのだ.」
A君「オームの法則を正しく使って計算すれば,抵抗や回路のイメージがさっぱりぱりぱりな僕でも,電気回路が解けるってこと?」
B君「そう.それどころか,正しく計算をしているうちに,回路の正しいイメージがどんどんできあがってくる.すごいでしょ.
そのために,暗算で計算をするのをおすすめしているわけよ.」
B君「てなわけで,電気回路(抵抗回路)の問題演習をしていこうか.」
すみませんページが増えすぎたので, その3へつづく