直列合成抵抗=R1+R2+R3+…
問1
合成抵抗はいくつか.
B君「力の合成 とは,どういうことか,説明できるかい?」
力の合成: 2つ以上の力を,それと同じはたらきをする1つの力にまとめることを,力の合成という.
で,その1つの力のことを,合力 という.
合成抵抗も,同じノリで定義できる.
合成抵抗:2つ以上の抵抗を,それと同じはたらきをする1つの抵抗にまとめたもの.
抵抗直列なら,簡単だよね.直列の合成抵抗は,単に足し算をすればよい.
直列合成抵抗=R1+R2+R3+…
問1
合成抵抗はいくつか.
合成抵抗=3Ω+5Ω=8Ωだ.
抵抗並列はちとややこしい.並列の合成抵抗は,「逆数の足し算の逆数」だ.
並列合成抵抗=
問2
合成抵抗はいくつか.
合成抵抗= =3Ωだ.
A君「並列の合成抵抗は,計算が面倒くさいよ.逆数にして,足し算して,また逆数にするなんて.」
B君「抵抗2本限定なら,並列合成抵抗はもっと簡単な公式があるよ.」
問3
合成抵抗はいくつか?
合成抵抗=
=2.4Ω
B君「抵抗回路の解き方にはね,ある程度,定石みたいなのがあるのだ.」
A君「例えば,抵抗並列回路の場合は?」
抵抗並列回路の解き方(よく使われる順に)
1.ふつうに解く
2.並列合成抵抗の公式を使って解く
B君「ほとんどの場合,ふつうに解く.ごくたまに,並列合成抵抗を使わないといけない場合が出てくる(後述)」
A君「定石もなにも,まったくふつうじゃん!」
B君「ここで,そもそも「ふつうの解き方」とは何なのか,を,確認しておこう.」
抵抗回路 ふつうの解き方
・オームの法則 ※V=RI の※Vは,「抵抗の両端の」電圧である.電池の電圧と同じとは限らない.
・抵抗1本につき,1つの※V=RIを立てる.
A君「抵抗2本の回路なら,※V=RI を2つ立てるわけか.」
B君「それではなるべく暗算で,問題を解いてみよう.」
問4
電圧が図のようになるのは,もうわかるよね.
それでは,ふつうに解くよ.
6Ωの抵抗について: 9V=6Ω×I1 I1=1.5A
3Ωの抵抗について: 9V=3Ω×I2 I2=3A
I1+I2=4.5A
または,
Iだけなら,合成抵抗の公式でも出せるよね.
合成抵抗=(6×3)/(6+3)=2Ω,
そして,合成抵抗の両端の電圧は9Vなので,
合成抵抗について: 9V=2Ω×I I=4.5A
A君「じゃあ,抵抗直列回路の場合は?」
抵抗直列回路の解き方(よく使われる順に)
1.分圧で解く
2.直列合成抵抗の公式を使って解く
(3.ふつうに解く ※めったにやらない)
B君「抵抗直列の場合,ほとんど1か2で解いてしまう.ふつうに解くことは,めったにやらない.」
A君「ふつうなのに,めったにやらないのか.なんでよ?」
例題1
まず,この回路を試しに,「3.ふつうに解く」で解いてみよう.
4Ωの抵抗について: V1=4Ω×I …①
2Ωの抵抗について: V2=2Ω×I …②
あと,電圧については,V1+V2=9V …③
①②③を連立して, I=1.5A V1=6V V2=3V だ.
A君「解けるじゃん.」
B君「今回は簡単だったけど,連立方程式を常に暗算で解ける人って,相当なスーパーマンだと思うよ.
連立方程式なんて,人間が解くもんじゃない.」
A君「じゃあ,どう解くのさ?」
B君「この問題なら,「1.分圧で解く」 が定石だろうね」
分圧とは?
抵抗直列回路では,電圧は抵抗の比に分圧される. 直列だけだよ
この回路を,「1.分圧で解く」で解いてみよう.
9Vを4Ω:2Ωに分圧するので,V1=6V V2=3Vだ.
そして,
4Ωについて: V1=4Ω×I V1を代入して,I=1.5A
B君「これなら暗算で出せるでしょ.」
※なぜ抵抗直列では電圧は抵抗の比に分圧されるのか?
水流モデルで説明しよう.
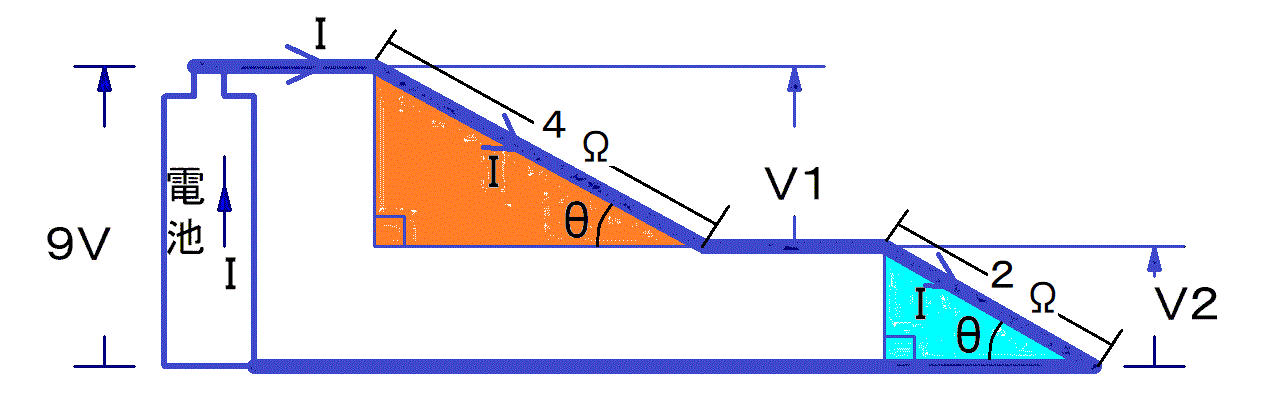
2つの抵抗に流れる電流Iは等しいので,2つのθも等しい.
つまり,図の2つの三角形は相似だ(二角)
だから,V1:V2=4Ω:2Ωになる.
抵抗直列では,電圧の比は抵抗の比と等しくなるのだ.
問5
まず,分圧で解いてみよう.
36Vを6Ω:7Ω:5Ωに分圧するのだから,V1=12V V2=14V V3=10V
V12=V1+V2=12+14=26V ってやってもいいけれど,
18分の13の分圧だと思えば,26Vだってすぐに出るよね.
そして,
6Ωの抵抗について: V1=6Ω×I V1を代入して,I=2A
または,
直列合成抵抗6+7+5=18Ωを使っても,解けるね.
合成抵抗の両端の電圧は36Vなので,
直列合成抵抗について: 36V=18Ω×I I=2A
6Ωについて: V1=6Ω×I Iを代入して,V1=12V
7Ω,5Ωについても同様 V2=14V V3=10V
B君「抵抗直列回路の場合,ほぼ100%,分圧で解くのが定石だ.合成抵抗を使うやりかたを知っておいてもいいけど.」
A君「ふつうに解くことは,やらないわけだね.」
B君「それでは,いきなりいくよ.問6と問7は,今の知識で解けるはずだ.」
A君「 なるべく暗算で,解くんだよね.」
問6
一応,水流モデルも書いてみたけど...まあ要らないかな.
分圧より,V3=8V
4Ωについて:16V=4Ω×I2 I2=4A
V4=16V+V3=24Vなのは,わかるよね(わからなければ,水流モデルを見て)
3Ωについて:V4=3Ω×I4 I4=8A
I=I2+I4=12A
2.5Ωについて:V1=2.5Ω×12A=30V
V=V1+V4=54V
問7
5Ωの両端と,10Ωの両端は,同じ電圧V2なのは,わかるね.
V2=5Ω×1A=5V
10Ωについて:V2=10Ω×I3 I3=0.5A
I=1A+I3=1.5A
4Ωについて:V1=4Ω×1.5A=6V
V=V1+V2=11V
例題2
A君「うーん,これは,どこからとりかかったらいいのか,わからないよ.」
B君「それではヒントだ. このような直並列回路は,分圧で解くのがセオリーだ.」
A君「うーん分圧? どこに抵抗直列回路があるっていうんだ...あ,もしかして,並列部分だけ合成抵抗にしちゃえばいいのか.」
B君「そう,部分的な合成抵抗をつくるのが,コツなのだ.」
10Ωと15Ωの部分の並列合成抵抗=(10×15)/(10+15)=6Ω
これで,2Ωと合成6Ωの抵抗直列回路が見えるね.12Vを2Ω:6Ωに分圧して,
V1=3V V2=9V
2Ωについて: V1=2Ω×I I=1.5A
10Ωについて: V2=10Ω×I2 I2=0.9A
I3=I-I2=0.6A
一応最後に,水流モデルを示しておくよ.
問8
なんか電池の向きとかを変えてあるけど,電気的には例題2と同じだよね.
30Ωと20Ωの部分の並列合成抵抗=(30×20)/(30+20)=12Ω
これで,8Ωと合成12Ωの抵抗直列回路が見えるね.15Vを8Ω:12Ωに分圧して,
V1=6V V2=9V
8Ωについて: V1=8Ω×I I=0.75A
30Ωについて: V2=30Ω×I2 I2=0.3A
I3=I-I2=0.45A
(応用)問9
抵抗R1の消費電力P1=37.5W,
抵抗R2の消費電力P2=25W,
抵抗R3の消費電力P3=12.5Wであった.
抵抗R1,R2,R3はそれぞれいくつ?
ヒント:R2とR3については,P=※VI または,P=I2R
2つの抵抗で,共通なのは何かな?
まず,R1はすぐにわかるね.P=※V2/Rより,
37.5=302/R1 R1=24Ω
次にR2とR3だけど,
P=※V×I 電流I2が共通なので,P2:P3=V2:V3なのは,わかるかな.
つまり,V2=20V V3=10V
あとはもうわかるよね.P=※V2/Rより,
25=202/R2 R2=16Ω
12.5=102/R3 R2=8Ω
(別解 ちょっとマニアック)
25W+12.5W=37.5Wなので,R1と,R2&R3の合成抵抗はおそらく同じ抵抗値だ.
だって,P=※V2/Rより,電圧※Vが同じで電力Pが同じなら,抵抗Rも同じでしょ.
R1は↑より24Ω つまり,R2+R3=24Ωだ.
で,R2とR3は電流I2が共通 P=I2Rより,P2:P3=R2:R3
つまり,R2=16Ω R3=8Ω
(応用)問10
電流I5はいくつか. 流れる向きが逆向きなら,マイナスで答えよ.
ヒント:部分合成抵抗
真ん中の部分は,左の回路と電気的に同じなのは,わかるかな.
単純に電線をどうつなぐかの違いだけだからね.
となると,この回路は,2つの部分合成抵抗の直列回路だってのは,わかるよね.
合成抵抗1=(6×2)/(6+2)=1.5Ω
合成抵抗2=(3×3)/(3+3)=1.5Ω
つまり,9Vを1.5:1.5に分圧 V1=4.5V V2=4.5V
6Ωについて: V1=6V×I1 I1=0.75A
以下同様に,I2=2.25A I3=1.5A I4=1.5A
となると,電流の収支から,I5=-0.75A(つまり,下から上へ電流が流れる)ってのは,わかるかな.
数式で示すなら,I1=I3+I5より,I5=-0.75A
問11
図で,スイッチS1をONにすると,各部の電流や電圧は?
ヒント:ONのスイッチは,電線(=水平パイプ)と同じ.
てきとーに解いても解けるだろうけれど,ちゃんとオームの法則に則って解いてみよう.水流モデルを見てごらん.
2Ωは,ONのスイッチS1(=水平パイプ)と並列なので,2Ωの両端は0Vとなる(2Ωのななめパイプは水平なので).
つまり,V1=0V で,V1+V2=12Vより,V2=12V
3Ωについて: V2=3Ω×I I=4A
2Ωについて: V1=2Ω×I1 I1=0A
I1+I2=Iより,I2=4A
ポイント
ONのスイッチや電線の両端の電圧は,0V(だって水平パイプだから)
問12
図で,スイッチS1をONにすると,各部の電流や電圧は?なお,I5は矢印の向きに電流が流れた場合を正とする.
スイッチS1の両端は0Vなので,V2=0V
で,V1+V2=9Vなので,V1=9V
6Ωについて: V1=6Ω×I1 I1=1.5A
2Ωについて: V1=2Ω×I1 I2=4.5A
3Ωについて: V2=3Ω×I2 I3=0A
電流の収支より,I1+I2=I3+I4 I4=6A
そして,I1=I3+I5より,I5=1.5A
問13
図で,スイッチS1をOFFにすると,各部の電流や電圧は?
A君「スイッチOFFなんでしょ.こんなの簡単だよ.」
B君「 本当に簡単だと思う?」
スイッチOFFなので,I=0だ.これはわかるね.
3Ωについて: V2=3Ω×I=0V
V1+V2=12Vなので,V1=12V
A君「V1が納得いかないよ.スイッチがOFFなんでしょ.0Vじゃないの?」
B君「実際にここに電圧計をつなげば,12Vを指すよ.やってみる?」
A君「納得いかないよ.スイッチが切れてたら圧力0なんだから0Vでしょうが!」
B君「君はまだ,電圧のことを圧力だと思っているのかい?高さの差だって言ってるでしょうが!」
V1+V2=12V この式は必ず成立しなければならない.
で,V2=0Vなんだから,V1は12Vになるのは,自明でしょ.
A君「うーん それでも納得いかないなあ.OFFのスイッチを∞Ωの抵抗だと考えたら?」
B君「V1=∞Ω×0A=不定値.だから,オームの法則では値が定まらない.で,V1+V2=12Vより,V1=12V」
A君「納得いかないよ」
B君「じゃあV1の位置に電圧計をつないでごらんよ.」 A君「12Vだ...」
例題3
図で,V1~V4はいくつか.
A君「もう暗算でわかるよ.9VをV1:V2=6Ω:9Ωに分圧するんだから,V1=3.6V V2=5.4V.
9VをV3:V4=4Ω:6Ωに分圧するんだから,V3=3.6V V4=5.4V あれれ同じだ.」
T君「じゃあ一般に,I5=0Aになるのは,R1~R4がどんなときかな?」
A点とB点の高さが同じになるときだから,
R2/(R1+R2)=R3/(R3+R4)のとき …④ だってのは,わかるかな.
B君「これでもいいけど,もっと簡単に考えようよ.
R1:R2=R3:R4のとき…⑤ でいいじゃん.」
A君「たしかに④と⑤は数学的に同じだね.⑤の方が使いやすいね.」