(改良型)水流モデル その4【高校範囲】キルヒホッフの法則で,より難しい抵抗回路を解こう【でも暗算には向かない】
1.キルヒホッフの法則の使い方
A君「キルヒホッフの法則って,何なのよ?」
B君「キルヒホッフの法則を使えば,どんな抵抗回路も解けてしまう,万能の法則だ.ただ,連立方程式を解かないといけないので,暗算には向かない.
今までこの法則を使わなかった理由はそれだ.」
A君「なるべくこの法則を使わず,暗算で解いてほしかったってことだね.」
B君「ただ,あるレベル以上の回路はキルヒホッフの法則など特殊な手法を使わないと解けないのと,キルヒホッフの法則の考え方自体はとても有用なので,
今回,解説をしてみようかと.」
例題1
一見すると難しそうだが,これは今までの知識で解けるはずだ.
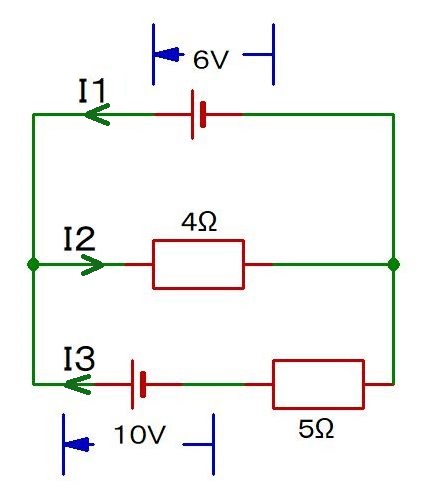
I1~I3はいくつ?
答はここをクリック
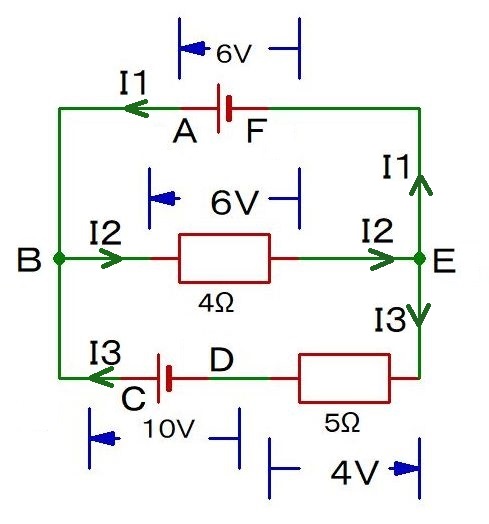 4Ωの両端の電圧が6Vになることは,わかるよね.
4Ωの両端の電圧が6Vになることは,わかるよね.
すると,5Ωの両端は4Vにならないといけないわけだ.わかるかな.
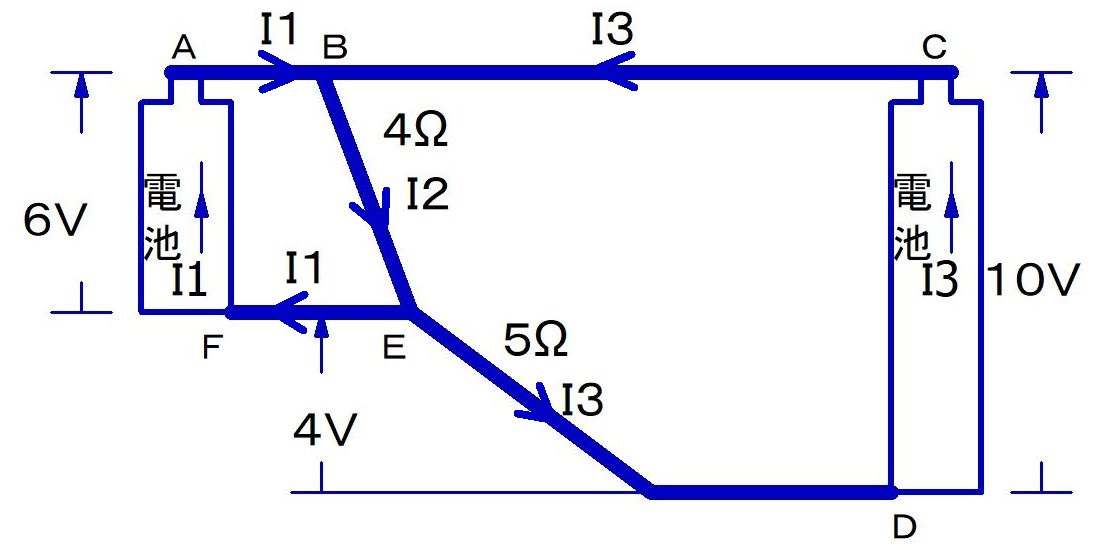 水流モデルで表すと,こんな感じだ.
水流モデルで表すと,こんな感じだ.
A君「5Ωの両端が4Vになることはわかったけど,この電圧の矢印が右を向くってのが,わからないよ.
5Ωの両端は,どちらも電池のマイナスにつながってるじゃん.これじゃわからないよ.」
B君「水流モデルを見れば,一発でしょ.電圧の矢印は,水流モデルの高い方につけるのだ」
A君「水流モデルを書けばわかるけどさあ,毎回こんなの書いてられないよ.」
B君「そうだね.回路の電池が2個以上の場合,電圧の矢印は今までのように「電池の+に(電気的に)近い方につける」っているルールでは,弱いんだよな.」
(より正しい)電圧の矢印の向きのルール(電池が2個以上の場合でも通用する)
1(新ルール): 抵抗の場合,抵抗に電流が流れ込む側(電流の入り口側)を矢印にする
2:電池の場合は,電池の+側を矢印にする.
3:水流モデルでは,高い方を矢印にする
4(新ルール):電圧計をつなぐときは,矢印の側を+端子(赤端子),反対側を-端子(黒端子)につなぐ

B君「今回は,電流I3は5Ωの右から左へ流れるので,4Vの電圧は右側を矢印にするのだ.」
A君「抵抗の場合,電流の矢印の向きと電圧の矢印の向きが結果的に逆になっちゃうのは,おもしろいね.
4Ωの両端の6Vも,電流I2が流れ込む側が矢印になってるね.」
A君「初めからこの正しいルールを教えればよかったじゃん」
B君「どうも中学生にはこれは難しいみたいでさあ」
A君「まあ考えてみれば,水はななめパイプを下から上へ自然に流れることはありえないから, 3.のルールを活かすためには,「1.ななめパイプの入り口側が矢印」なのは当然なのか.」
あとはまあ,計算すればわかるよね.
4Ωについて: 6V=4Ω×I2 I2=1.5A
5Ωについて: 4V=5Ω×I3 I3=0.8A
I2=I1+I3より,I1=0.7A
さて,キルヒホッフの法則は,第1法則と第2法則の2つからなるのだけれど,
まずは重要な第2法則から,確認していこう.

たとえば,A→B→E→F→A と,1周してみよう.初めと同じ高さになるよね.
A→B → E →F → A
0 -6V +0 +6V =0
たとえば,F→E→D→C→B→A→F と,1周してみよう.
F→E → D → C →B →A → F
0 -4V +10V +0 +0 -6V =0
初めと同じ高さになるよね.
このように,水流モデルを1周すると,必ず,初めと同じ高さになる.
どこからスタートしても,どっち向きに廻っても,初めと同じ高さになる.
A君「当たり前じゃないか」
B君「その当たり前が,キルヒホッフの第2法則なのさ.」

次は,回路図でやってみよう.
電圧の矢印の向きに進むと,高くなり,
電圧の矢印と逆向きに進むと,低くなる.
これは,水流モデルから明らかだよね.
たとえば,B→A→F→E→B と,1周してみよう.
B→A → F →E → B
0 -6V +0 +6V =0
初めと同じ高さになるよね.
たとえば,C→D→E→B→C と,1周してみよう.
C → D → E → B →C
-10V +4V +6V +0 =0
初めと同じ高さになるよね.
A君「だから何なのさ」
B君「このテクニックを使えば,I1~I3を数学的に導くことが,できるんだよ.」
具体的には,抵抗部分にオームの法則を使ってみる.※V=RIだな.
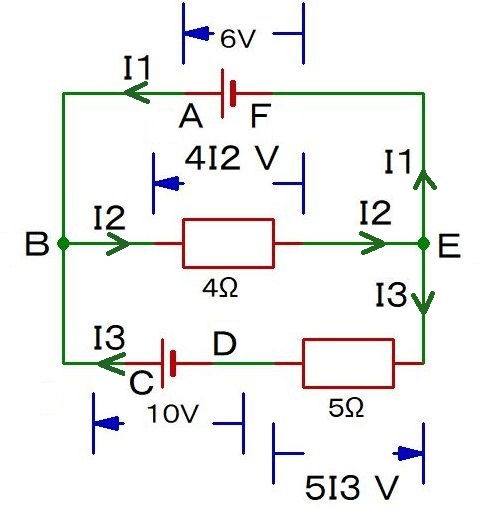
あ,せっかくだから,キルヒホッフの第1法則も導入してしまおうか.
キルヒホッフの第1法則(改):電流の数は,囲まれたエリアの数だけ定義すればよい.それ以上は足し算引き算でなんとかするべし.
たとえばこの回路の場合,電線などで囲まれたエリアは2つある.だから,電流は2つ定義すればよい.3つも要らないのだ.
だから,1つ減らすよ.どれを減らしてもいいけど,I1=I2-I3なので,I1をカットして,I2とI3だけの式にしよう.
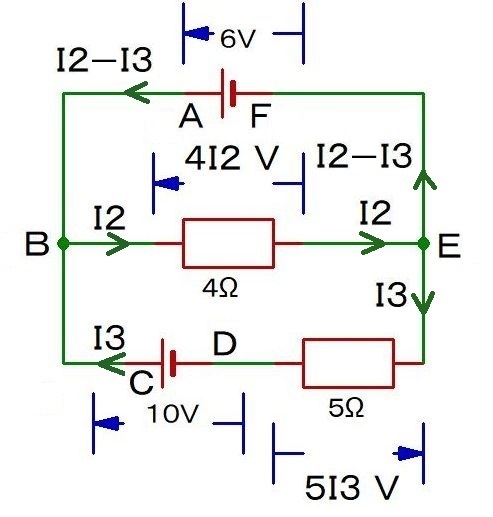
そして,キルヒホッフ第2法則だ.
キルヒホッフの第2法則(改):
1.電池部分は電池の電圧,抵抗部分はオームの法則※V=RIで,各部の電圧を書く.
2.1周すれば,必ず初めと同じ高さになる.
3.エリアの数(=定義した電流の数)だけ,周回する.ただし,回路のすべての部分を最低1回は通るようにしないといけない.2回以上通ってもよい.0回はダメ.
どっち回りでもいいし,どこからスタートしてもよい.
4.すると,エリアの数(定義した電流の数)だけ式が立つはずなので,連立方程式で解く.
今回の場合,エリアが2つなので,周回を2つ行う.
好きな周回経路を選んでくれてよい.たとえば
B→E→D→C→B: -4I2-5I3+10=0 …①
A→B→E→F→A: -4I2+6=0 …②
回路のすべての部分を最低1回は通ったので,OK.
で,①②を連立して, I2=1.5A I3=0.8Aだ.
I1=I2-I3=0.7A
ほら,数学的にI1~I3を出せたでしょ.
B君「これが,キルヒホッフの法則を使った,回路の解き方だ.」
A君「ふーーーーん めんどくさい.連立方程式だから暗算も使えないし.こんなの使わなくてもいいじゃん.」
例題2
B君「この例題2は,キルヒホッフの法則を使わないと解けまい!」
A君「そんなの要らないよ.ちょちょいっと....うっ 何だこれは」
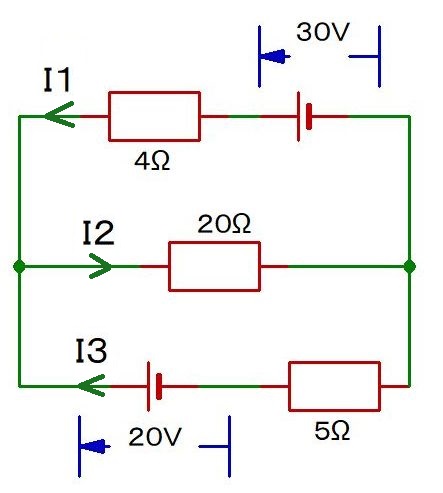
I1~I3はいくつ?
答はここをクリック
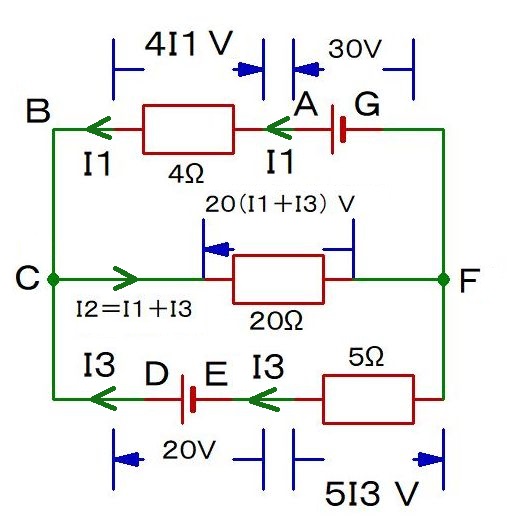
まず,キルヒホッフの第1法則.
電線などで囲まれたエリアは2つなので,電流の定義を2つにしちゃうよ.
今回はI2=I1+I3より,I2をカットして,I1とI3だけにしちゃおう.
次に,キルヒホッフの第2法則.今回の場合,エリアが2つなので,周回を2つ行う.
どんな周回コースでもいいんだけどさ,たとえば,
A→B→C→D→E→F→G→A: -4I1-20+5I3+30=0 …①
C→F→E→D→C: -20(I1+I3)-5I3+20=0 …②
もすこし整理して,
4I1-5I3=10 …①
4I1+5I3=4 …②
①②を連立して,I3=-0.6A I1=1.75A
I2=I1+I3=1.15A
A君「I3がマイナスだよ!」
B君「つまりI3は,図の電流矢印とは逆向きに電流が流れるってことだよ.」
A君「そんなことしたら,20Vの電池は充電されちゃうじゃないか.いいのかよ?」
B君「理想電池は充電もできるのさ.」
A君「むちゃくちゃだよ!」 B君「君は○ネループを否定するのかい?」
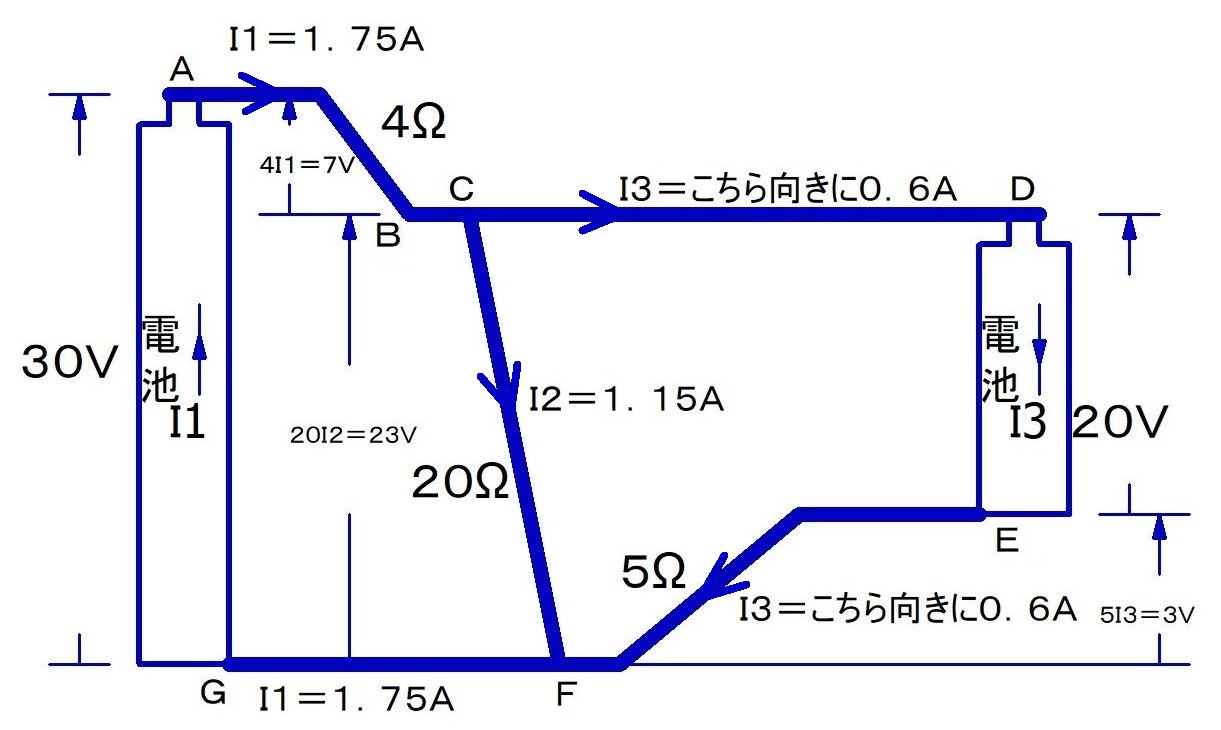
水流モデルで示すと,こんな感じ.
5Ωのななめパイプを見ると,電流I3は必ず上から下へしか流れないので,
I3はこの向きにならないといけない.つまり,20Vの電池が充電されちゃうのはやむを得ないのだ.
2.それでは問題演習だ.キルヒホッフの法則を使って,難しい抵抗回路を解こう
問1
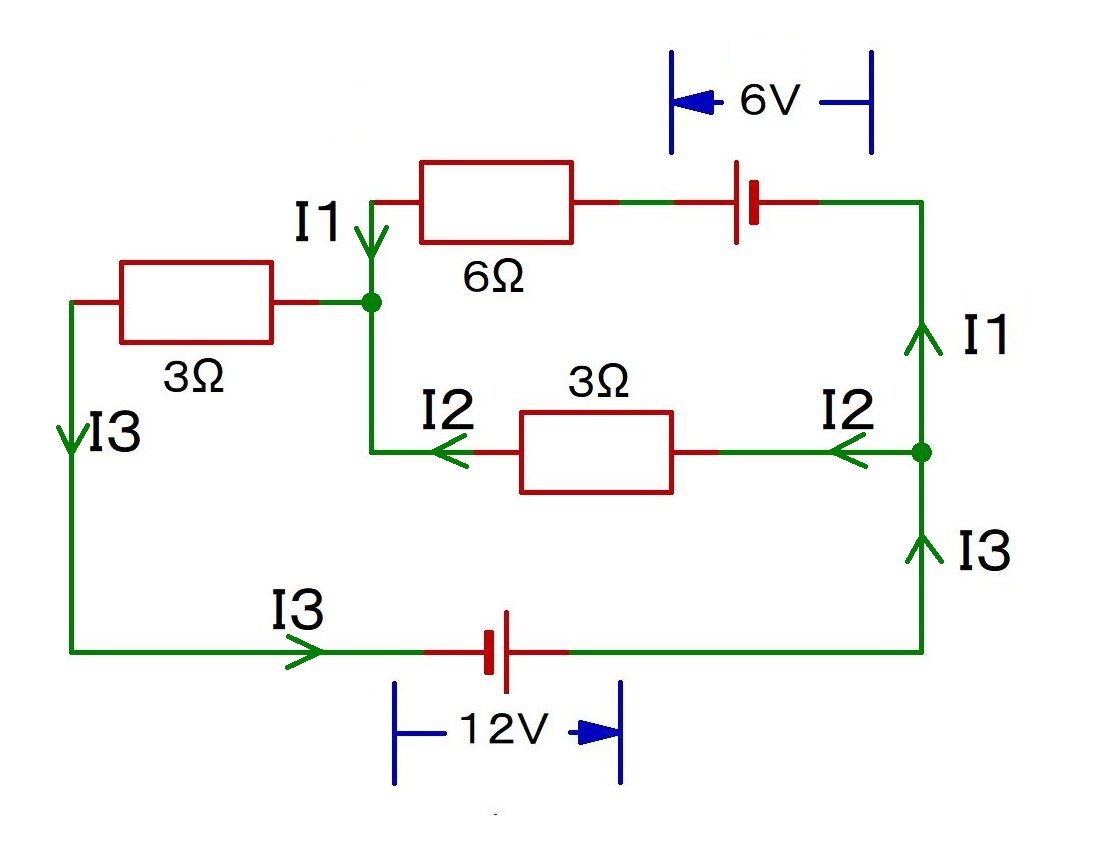
I1~I3はいくつ?
答はここをクリック
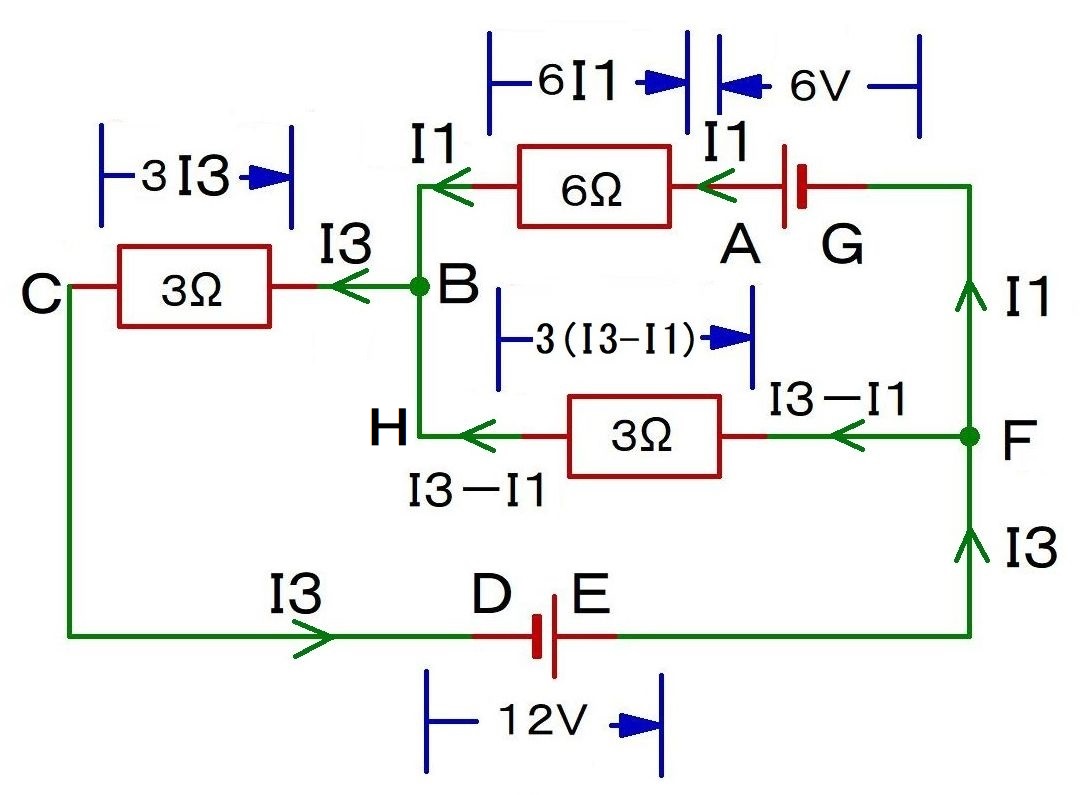
まず,キルヒホッフの第1法則.
電線などで囲まれたエリアは2つなので,電流の定義を2つにしちゃうよ.
今回はI1=I2+I3より,I2をカットして,I1とI3だけにしちゃおう.
I2=I3-I1だね.
次に,キルヒホッフの第2法則.今回の場合,エリアが2つなので,周回を2つ行う.
どんな周回コースでもいいんだけどさ,たとえば,
A→B→H→F→G→A: -6I1+3(I3-I1)+6=0 …①
C→D→E→F→G→A→B→C: +12+6-6I1-3I3=0 …②
もすこし整理して,
3I1ーI3=2 …①
2I1+I3=6 …②
①②を連立して,I1=1.6A I3=2.8A
I2=I3-I1=1.2A
問2
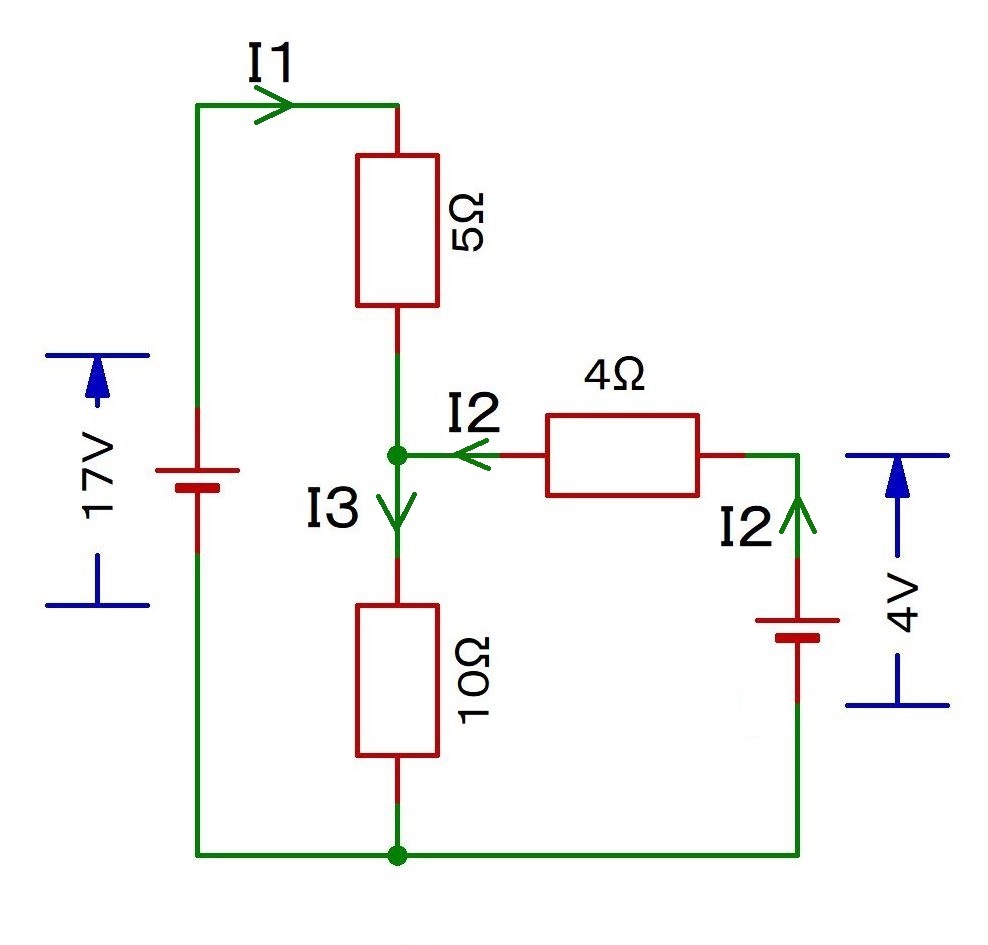
I1~I3はいくつ?
答はここをクリック
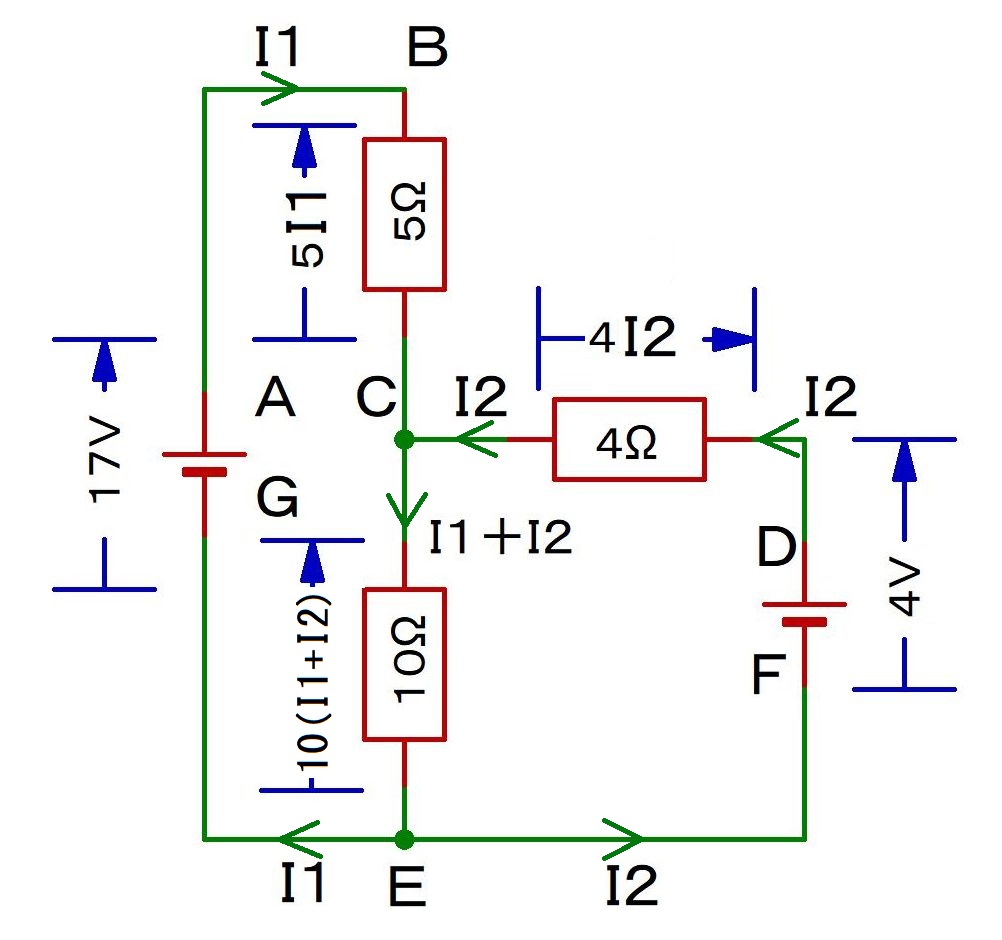
まず,キルヒホッフの第1法則.
電線などで囲まれたエリアは2つなので,電流の定義を2つにしちゃうよ.
今回はI3=I1+I2より,I3をカットして,I1とI2だけにしちゃおう.
次に,キルヒホッフの第2法則.今回の場合,エリアが2つなので,周回を2つ行う.
どんな周回コースでもいいんだけどさ,たとえば,
A→B→C→E→G→A: -5I1-10(I1+I2)+17=0 …①
F→D→C→E→F: +4ー4I2-10(I1+I2)=0 …②
もすこし整理して,
15I1+10I2=17 …①
10I1+14I2=4 …②
①②を連立して,I1=1.8A I2=-1A
I3=I1+I2=0.8A
問3
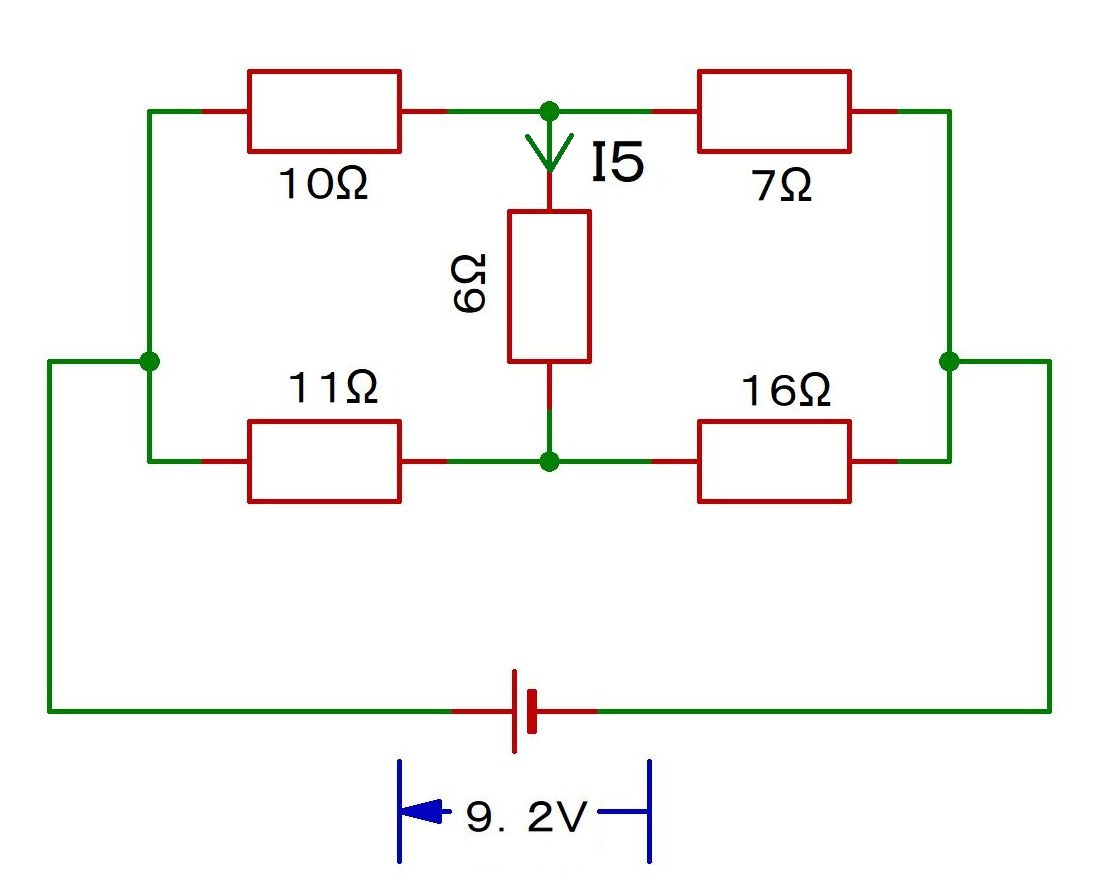
I5はいくつ?
答はここをクリック
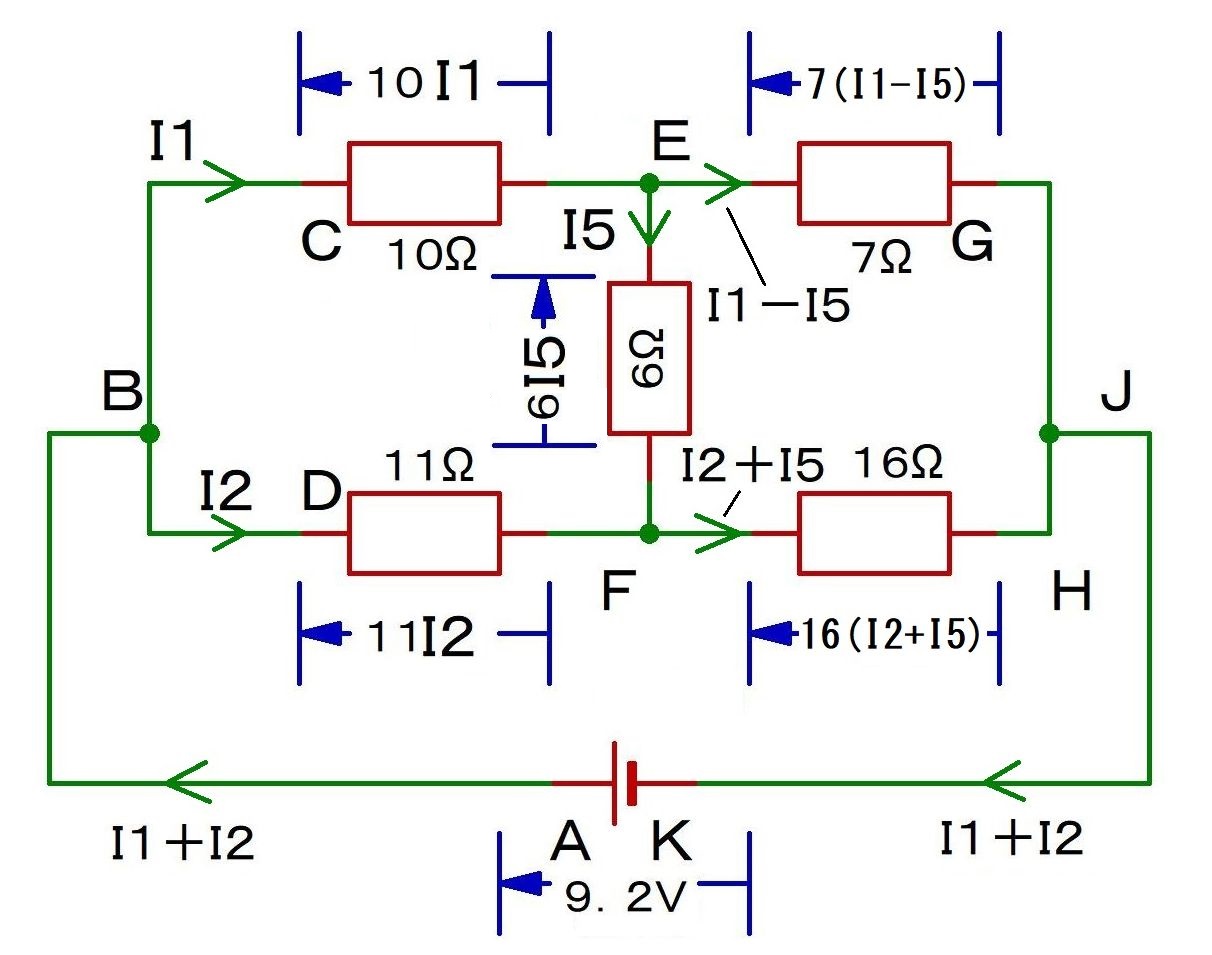
まず,キルヒホッフの第1法則.
さすがに電流I5だけでは解けない.電線などで囲まれたエリアは3つなので,電流の定義を合計3つにしちゃうよ.
図のように,I1,I2,I5の3つで解こうか.
次に,キルヒホッフの第2法則.今回の場合,エリアが3つなので,周回を3つ行う.
どんな周回コースでもいいんだけどさ,たとえば,
A→B→C→E→G→J→K→A: -10I1-7(I1ーI5)+9.2=0 …①
C→E→F→D→C: -10I1-6I5+11I2=0 …②
E→G→H→F→E: -7(I1-I5)+16(I2+I5)+6I5=0 …③
もすこし整理して,
-17I1+7I5=-9.2 …①
ー10I1+11I2-6I5=0 …②
ー7I1+16I2+29I5=0 …③
①②③を連立して,I1=0.5A I2=0.4A I5=-0.1A
つまり,I5=-0.1Aだね.
A君「こんな3元連立方程式なんて,解きたくないよ.かんべんしてよ.」
B君「そう言われましても...キルヒホッフの法則と連立方程式は,切っても切れない関係だからねえ.」
3.重ね合わせの理 とか,鳳テブナンの定理とか
キルヒホッフの法則を使うと,連立方程式を使わないといけなくなっちゃう.
もっと楽に,難しい回路を解く方法は,ないだろうか.
キルヒホッフの法則のように「万能」ではないけれど,
ある種の回路を楽に解く手法ってのは,いくつかあるんだ.
ここではまず,
重ね合わせの理 を,紹介しよう.
電池が2つ以上ある回路を,楽に解く手法だ.
たとえば問1や問2は,重ね合わせの理 でも解ける.

試しに,問1を解いてみようか.
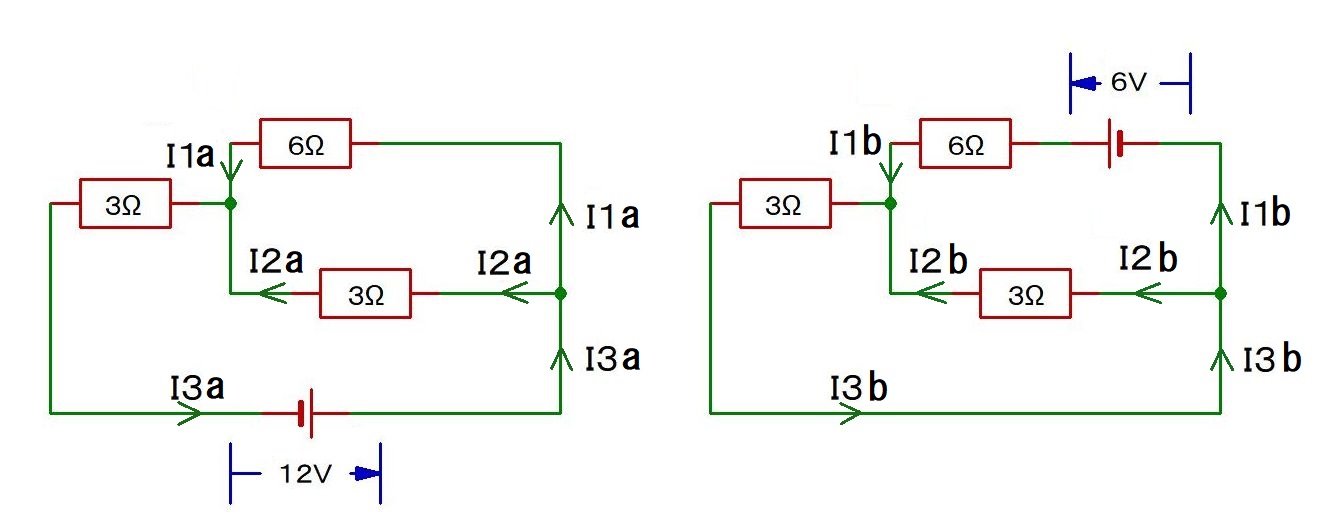
問1は,左の2つの回路(電池がそれぞれ1個ずつの回路)が
重なり合っている,と考えるのだ.
I1a,I2a,I3a,I1b,I2b,I3bは,暗算でも出せるでしょ.
A君「暗算...まあ,やればできるか.」
I1a=0.8A I2a=1.6A I3a=2.4A
I1b=0.8A I2b=-0.4A I3b=0.4A ●I2bがマイナスだってことに注意ね
B君「で,このaとbを足し算(重ね合わせ)すればOK」
I1=1.6A I2=1.2A I3=2.8A
ほら,キルヒホッフの法則よりもずっと楽に出せるでしょ.
問2も,重ね合わせの理で解いてごらん.
A君「問3は電池が1個だから,重ね合わせの理では解けないね.」
B君「そうだね.問3のような回路は,鳳-テブナンの定理 が楽だぜ. ほうてぶなんのていり と読む.鳳秀太郎(ほうひでたろう)先生の名前からきてるのだ.」
A君「どんな定理?」
B君「えっとね...忘れた.毎回やりかたを覚えて,すぐに忘れるんだよなこれ...」
興味があれば,調べてごらん.いろんな人がHPでわかりやすく解説してるよ.
A君「ポテチン」「それは鳳啓助(おおとりけいすけ)さんだ」
(もくじに戻る)
4Ωの両端の電圧が6Vになることは,わかるよね.
水流モデルで表すと,こんな感じだ.